Kompleks systemteori og dens implikasjoner
Skrevet av: Elizabeth Normann- bachelor student i psykologi ved NTNU
Komplekse system er overalt rundt oss. De manifesterer seg i hvordan migrerende fugleflokker organiserer seg og hvordan mennesker danner sosiale nettverk. Komplekse systemer kan gjenkjennes i strukturen til planter, snøflak og hvordan galakser organiserer seg. De eksemplifiseres i urban utvikling og i aksjemarkedets svingninger. Den lineære virkelighetsoppfatningen til mennesker påvirker hvordan vi forstår komplekse systemer. Komplekse system er universelle, de eksisterer på alle arenaer og analysenivåer. Fellestrekket til slike komplekse systemer er en balanse mellom orden og kaos. De er både forutsigbare og uforutsigbare. For optimal fungering av komplekse system kreves en balanse mellom disse to motstående kreftene. En ubalanse vil føre til et patologisk system.
Teorien om komplekse systemer utfordrer den tradisjonelle vitenskapelige metoden. Den tradisjonelle metoden reduserer og analyserer virkeligheten til noen få forutsigbare variabler i lineære systemer. Konfrontert med hjernens kompleksitet er lineære modeller utilstrekkelige for inferens. Hvordan kan vi anvende kompleks systemteori for å bedre forståelsen av hjernen og menneskelig patologi?

Det newtonianske paradigmet og reduksjonisme
De spørsmålene vi mener er viktige å stille, de metodene vi anser som riktige for å konkludere, og de resonneringsprosessene menneske mener er valide, er avslørende for hvilke antagelser vi har om hvordan verden fungerer. Med vitenskapelig forskning forsøker man å beskrive fenomen ved å samle empirisk data og utvikle logiske og konsistente teoretiske modeller for å kunne tolke mønstre. Vitenskapelig undersøkelse gjennomføres i kontekst av paradigmer. Et paradigme er et sett bestående av antagelser som styrer hvordan vi interagerer med og tolker verden. Den moderne vitenskapelige metode har i stor grad blitt formet av det newtonianske paradigmet. Det er best karakterisert ved sitt materialistiske syn på objekter, og med lineære årsak-effekt interaksjoner (Colchester, 2016). Det er dette som gir forståelsen av universet analogt til en stor maskin eller klokke, hvorav begge anses som ordnede og predikerbare. I dette paradigmet kan vi forstå universet ved å forstå dets bestanddeler og de lineære interaksjonene mellom dem. Denne undersøkelsesprosessen er det som refereres til som reduksjonisme.
Den nobelprisvinnende hjerneforskeren Eric Kandel (2016), har dratt linjer mellom hvordan både forskere og kunstnere bruker reduksjonisme. Destillasjon av større vitenskapelige eller estetiske konsept til mindre, mer medgjørlige komponenter i deres respektive søk etter sannheten. Innenfor den kunstneriske bevegelsen abstrakt ekspresjonisme utfordrer malere visuell representasjon ved å redusere bilder til deres grunnleggende forståelse av elementer med fokus på form, farge og lys. På samme måte har vitenskapelig reduksjonisme søkt etter å forklare komplekse fenomen ved å dekomponere prosessen på et mer elementært og mekanistisk nivå.
For å tydeliggjøre hva et komplekst system er, er det viktig å skille mellom begrepene kompleks og komplisert. Kompliserte problemer kan være vanskelige å løse, men de kan adresseres med regler, algoritmer, systemer og prosesser. Komplekse problemer kan på den annen side involvere ukjente enheter, i tillegg til at det kan eksistere for mange interagerende faktorer til at problemet kan reduseres til enkle regler og prosesser (Kinni, 2017). Når mennesker ønsker å forstå et komplekst system forteller vår intuisjon at vi skal dekomponere problemet, ved et standard oppsett som resonnerer lineær tenkning. Denne tilnærmingen viser seg å være utilstrekkelig for å forstå problemet. Slik lineær tenkning blir reduksjonistisk, hvor reduksjonisme fungerer som en analytisk strategi som forsøker å forklare de ulike komponentenes funksjon. Til slutt summeres forståelsen for funksjonene for å forstå den overordnede funksjonen.
Det er dog relevant å skille mellom grådig og hierarkisk reduksjonisme. Grådig reduksjonisme handler om å redusere forklaringer av alle typer atferd til det laveste analysenivået. Hierarkisk reduksjonisme beskriver derimot at det eksisterer ulike analysenivå for å forklare dynamikken av et gitt system, hvor det laveste analysenivået ikke nødvendigvis er det beste. Kompleks systemteori beskriver at for å oppnå en presis forståelse av et komplekst system vil analyse av de høyere nivåene fungere bedre enn de lavere nivåene. Denne typen systemteori er ikke grådig reduksjonistisk fordi det tar hensyn til det faktum at når man legger sammen flere tilknyttede elementer finner man noe annet enn den konvensjonelle oppfatningen av det forventede, og det skapes en kvalitativ ny egenskap vi kaller emergens.
I teknisk forstand kalles det newtonianske paradigmet for lineær systemteori (Colchester, 2016). Lineær systemteori håndterer relativt enkle systemer som har en begrenset mengde uavhengige, homogene elementer som interagerer på en veldefinert måte, som samtidig har et mindre antall tilknyttede elementer. Slike simplistiske systemer er ulike fra komplekse systemer blant annet grunnet antall interagerende elementer som utgjør systemet. Kvantitative forskjeller fører til kvalitative forskjeller (Anderson, 1972).
Flere tilknyttede elementer produserer kvalitativt nye egenskaper, og har en nedadgående effekt på delene som utgjør systemet (i.e. top-down kausalitet). Komplekse systemer karakteriseres av emergens, som betyr at den atferden systemet manifesterer kan ikke reduseres til atferd av dets komponenter. I boka Scale forklares dette med at ”i mange tilfeller virker det som helheten foretar sitt eget liv, nesten disassosiasert fra de spesifikke karakteristikkene av dets individuelle bygningsblokker” (West, 2017).
Sentralt for den historiske og konseptuelle utviklingen av kompleks systemteori er kaosteorien. Meteorologen Edward Lorentz (1963) er kjent som grunnleggeren av moderne kaosteori. På begynnelsen av 60-tallet observerte meteorologen at små forskjeller i en tilstand kan utløse store og uforutsigbare resultater (f.eks ”butterfly effect”). Professor Lars Folke Olsen har formulert det følgende: ”Før (Lorentz sin artikkel) kom frem trodde man at hvis man bare kjente tingenes begynnelsestilstand, deres posisjoner og hastighet, så kunne man forutsi dem i all fremtid. Lorentz viste at med et simpelt system med kun tre variabler, så kan man ikke forutsi noe som helst” (sitert i Bendix, 2013). På denne måten har Lorentz formulering av kaosteori bygget bro mellom det tilfeldige og det uforutsigbare og dermed bidratt til å presisere dynamikken til komplekse systemer.
Selvorganisering og nevral plastisitet
Komplekse system karakteriseres av selvorganisering, et grunnleggende konsept som bryter med den mye brukte data-analogien om hvordan hjernen fungerer. Datamaskiner er designet med en spesifikk mal som fullstendig spesifiserer hvordan de ulike delene skal samarbeide sammen. Design av hjernen derimot, er styrt av selvorganisering. Gjennom samhandling med miljøet muliggjøres optimal utvikling i henhold til miljøets krav. Genomet fungerer ikke som en mal, men heller som en generator hvor systemet skaper proteiner, som videre skaper nye strukturer for at mennesker kan fungere optimalt i ulike miljøer. Konsept som selvorganisering er grunnleggende for presis forståelse av dynamikken til komplekse systemer.
Komplekse systemer er svært robuste. Ta en maurkoloni som et eksempel. Dersom du fjerner en stor andel maur vil de resterende ta over oppgaven for de som har forsvunnet. Det samme konseptet gjelder hjernen, hvor nevral plastisitet bidrar til funksjonell rehabilitering ved skade. Etter et slag vil for eksempel plastiske endringer inkludere nydanning samt endring av funksjonen til eksisterende synapser, kortikal reorganisering og muligens også nydanning av hjerneceller (Dietrichs, 2007). Dermed kan man forstå nevral plastisitet som det sentrale nervesystemets evne til å tilpasse seg eksterne og interne påvirkninger på en hensiktsmessig måte, i regi av selvorganisering.
Slik selvorganisering ser man ikke i enklere systemer. En mekanisk klokke, for eksempel, består av flere unike komponenter med designerte oppgaver. Dersom man fjerner en del av de tilhørende enhetene vil klokken slutte å fungere. Det som er vesentlig for fleksibilitet og robusthet i komplekse systemer er dermed at de består av både orden og kaos. For eksempel, i midten av en bikube vil det alltid være 45 grader (Wiesner, 2015). Dersom en bie merker at det blir kaldere vil den bevege på seg for å forsøke å øke temperaturen. Dermed har man en ikke-predikerbar atferd på lavere nivå i systemet som bidrar til å opprettholde en betinget stabilitet, på et høyere nivå i systemet. Det er dog ingen sentral kontrollør for dette komplekse systemet. Det er derimot en koordinert samhandling mellom komponentene som styrer atferden i et komplekst system.
Scott Kelso (1995) sin beskrivelse av hjernen bryter med den klassiske data-analogien som ofte er det konvensjonelle operative rammeverket for psykologiske og nevrofysiologiske studier. Hans tese er at skapelse og utvikling av mønstret atferd ved alle nivå, fra nevronet til sinn, er styrt av generiske og selvorganiserende prosesser. Både hjernen og atferd fremviser trekk av mønsterformende dynamiske systemer som har tre grunnleggende kjennetegn. En av de er multistabilitet. Multistabilitet innebærer å ha flere stabile likevektstilstander. Det andre kjennetegnet er raske faseoverganger, hvor det foregår hurtige overganger mellom de ulike stabile likevektstilstandene. Det tredje er periodisitet, som er regelmessig tilbakevending av visse fenomener innenfor bestemte tidspunkter. Kelso viser at den menneskelige hjernen er fundamentalt et mønsterformende dynamisk system på kanten av ustabilitet.
Nevrale oscillasjoner og fraktalteori
Emergens i komplekse systemer manifesterer seg som strukturerte makroskopiske mønstre, og er konsekvensen av uavhengige mikroskopiske interaksjoner mellom komponentene i systemet. Slike makroskopiske mønstre manifesteres i hjernen som hjernebølger, eller nevrale oscillasjoner. Nevrale oscillasjoner er rytmiske mønstre av nevral aktivitet i og på tvers av hjerneregioner. De nevrale oscillasjonene fremmer presis temporal koordinering av de nevrale prosessene som underligger kognisjon, hukommelse, persepsjon og atferd (Neustadter, Mathiak og Turetsky, 2016). I den innflytelsesrike boken Dynamical Systems in Neuroscience (Izhikevich, 2007) forklares det hvordan synkronitet i kortikale nettverk skaper nevrale oscillasjoner ved ulike frekvenser slik som alfarytme (8-12 Hz) og gammarytme (40 Hz), som er assosiert med viktige funksjoner som oppmerksomhet og arbeidsminne. Det er frekvenssynkronisering mellom nevrale nettverk som muliggjør utførelsen av slike oppgaver. Dette er komplekst fordi oscillasjonene er ikke-lineært relaterte. Oscillasjonenes temporale organisering forekommer på flere tidsskalaer samtidig.
I tillegg til rytmisk atferd, indikerer forskning at noen fysiologiske (e.g. hjerterytme) og atferdsmessige (e.g. lokomosjon og sosial atferd) prosesser demonstrerer robuste skala-invariante selv-lignende mønstre. For å forstå hva skala-invariante selv-lignende mønstre betyr, er det nødvendig med en gjennomgang av fraktalteori. Kystlinjeparadokset er en god illustrasjon på fraktalteori, og beskriver den kontraintuitive observasjonen at lengden på en kystlinje avhenger av hvilken målestokk man bruker (Weiner, 2018). Jo mindre målestokken er, jo lengre blir kysten. Teoretisk kan man undersøke lengden av en kystlinje på et molekylært nivå, men da vil lengden nærme seg uendelig. Dette er fordi kystlinjen har fraktale egenskaper. Fraktal geometri brukes for å beskrive ikke-målbare former i naturen. Eksempler på andre fraktale fenomen er trær, lyn, snøfnugg, krystaller, blodårer og nevroner. Fraktale strukturer kjennetegnes med bifurkasjon, som vil si punktet eller området hvor noe deles inn i to deler.
Fraktaler er selv-lignende på flere nivå, og kan dermed beskrives som skala-invariante. Et objekt er geometrisk selv-lignende når mindre deler av objektet er eksakt, eller tilnærmet lik hele objektet. En liten del av en kystlinje ligner på en større del av en kystlinje. Statistisk selv-likhet gjelder biologiske objekter, inkludert alle anatomiske former. Mindre deler, som konstituerer et anatomisk system, er sjeldent identiske kopier av hele systemet, men ofte ganske likt. Grener har den samme strukturelle kompleksiteten som et helt tre. Også vaskulære årer ser like ut, uavhengig av hvilken skala du ser på (Di leva, Grizzi, Jelinek, Peiionisz og Angelo Losa, 2014).
Fraktale systemer utvikles historisk, noe som betyr at deres fortid eller historie (for eks erfaring) tillegges og determinerer fremtidig bane. Dessuten vil emergent atferd spille en determinerende rolle i utviklingen av systemet, altså top-down kausalitet, noe som er grunnen til at slike system fremviser stor grad av uforutsigbarhet (Fryer og Ruis, 2014). Den selv-lignende egenskapen av fraktaler er det som definerer at de er skala-invariante.
Når man anvender fraktaler til tidsserier ser man selv-lignende temporale fluktueringer på tvers av flere tidsskalaer. Slik skala-invarians er viktig for fysiologi og biokjemi fordi de avslører en intern felles avhengighet blant de ulike funksjonelle organiseringsnivå hos levende systemer (Guzman, Fleisa, Aon, Pellegrini, Marin og Kembro, 2017). Nevroner er organisert i mikronettverk og makronettverk som har fraktal struktur. Skala-invarians i nervesystemet muliggjør samarbeid på tvers av ulike frekvensbånd som er ansvarlige for ulike oppgaver (f.eks arbeidsminne), samt ulike nevrale moduler (e.g. primære sanseområder).
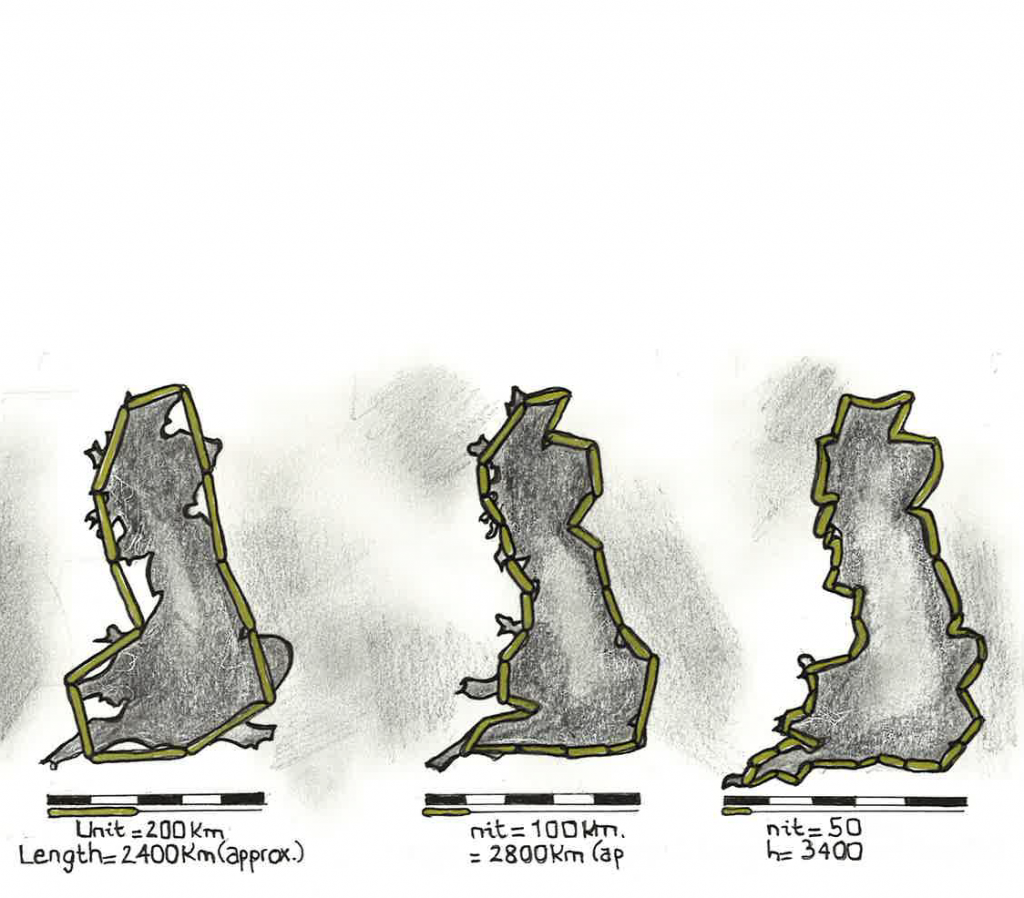
Illustrasjon: Miriam Billaud Feragen
Kompleksitet i nevrologi og psykiatri
Kaos har en viktig plass i kompleks systemteori fordi et komplekst system eksisterer på et spektrum som spenner seg fra likevekt til kaos. Et system i likevekt har ikke den interne dynamikken som muliggjør respons til miljøet (Fryer og Ruis, 2004), og vil dermed forbli statisk. Et system i kaos vil opphøre å være et system. Den mest produktive tilstanden å være i vil dermed være på kanten av kaos, som muliggjør kreativ tilpasning og løsninger til utfordringer systemet møter på. Selvorganiseringen som muliggjør nevral plastisitet fordrer både fleksibilitet (hebbiansk plastisitet) og robusthet (homeostatisk plastisitet). Men dersom komplekse systemer er så robuste, kan det reises spørsmål ved hvordan avvik fra optimal fungering forekommer.
Fra et klinisk standpunkt er det viktig å undersøke og analysere hjernebølger ved nevral dysfunksjon. Forskning er nemlig ikke entydig på om tilstedeværelse av kaos i nevrale oscillasjoner er assosiert med patologi. Nevrale oscillasjoner karakteriseres av rytmisk aktivering av store nevrale populasjoner i ulike temporale og spatiale skalaer, og muliggjør informasjonsprosessering og overføring. Støy er en allmenn forekomst i det sentrale nervesystemet. Støy er ofte oppfattet som forstyrrende faktor i en forskningssammenheng, men tilfeldige forstyrrelser eller støy tilført i optimale mengder kan faktisk fremme informasjonsoverføring i hjernen (Sannita, 2008). På denne måten bidrar kaos og orden til optimal fungering av systemet.
Utenom støy er det en annen form for kaos som er nødvendig for optimal fungering av det sentrale nervesystemet, nemlig ustabilitet. Ustabilitet er en kompleks tilstand som formelt kalles kritikalitet. Ved kompleks hjerneaktivitet eksisterer det nevrale skred ved alle spatiale og temporale skalaer. Den danske fysikeren Per Bak (1987) introduserte begrepet selvorganisert kritikalitet, et prinsipp som beskriver en enkel sandhaug, hvor skred av ulike størrelser hjelper med å holde systemet stabilt. Korn for korn vil sand akkumuleres. Etterhvert vil den voksende haugen nå et punkt hvor det vil være så ustabil at en marginal økning vil føre til kollaps i form av et skred. Basen utvides, og sandhaugen bygges opp igjen til det kritiske punktet slik at et nytt skred forekommer. Det er gjennom denne serien av skred av ulik størrelse at sandhaugen, et komplekst system av millioner av små elementer, vedlikeholder helhetlig stabilitet. Selvorganisert kritikalitet har blitt foreslått som forklaring på fraktal skalering i mange naturlige systemer, inkludert det nevrale systemet (Favela, Covey, Griff og Richardson, 2016)
Bak publiserte senere boken How Nature Works (1996), hvor han anvendte det prinsippet til andre komplekse systemer som jordskjelv, distribusjon av galakser i universet, og ikke minst, hjernen. Baks hypotese er at hjernen befinner seg konstant på eggen av en faseoverføring, mellom orden og kaos. Nevrale skred, altså kaskader av kompleks hjerneaktivitet, er avgjørende for en hjerne med raske overganger mellom ulike kognitive tilstander og motoriske programmer. For et levende system som hjernen er selvorganisert kritikalitet en mekanisme for å utføre raske kalkulasjoner, ikke ulikt selvorganiserende atferd av finansielle markeder som raskt klarerer priser (Frolich, 2016). For hjernen er tap av kritikalitet, patologisk. Med andre ord vil kompleks atferd observert i hjerneaktivitet kunne anvendes som biomarkør for sykdomsrisiko eller prognose. Ved bruk av matematiske verktøy som kvantifiserer kompleksitet har forskere ved ledende institusjoner over hele verden identifisert potensielle biomarkører for psykiatriske lidelser som autisme og schizofreni i EEG-signaler (Frolich, 2016).
Nevrale skred er en mekanisme hvor et komplekst system unngår å bli fanget i en av de to ekstremtilfellene: fullstendig orden og fullstendig kaos. The International League Against Epilepsy (ILAE) definerer et epileptisk anfall som en flyktig forekomst av symptomer grunnet overstadig konsentrert nevral aktivitet eller synkron nevral aktivitet i hjernen. Epilepsi forårsakes altså av for mye orden. EEG-målinger hentet fra epilepsipasienter avslørte at de kritiske nevrale skredene forsvant midt under anfallet (Meisel, Storch, Hallmeyer-Elgner, Bullmore og Gross, 2012). Slik patologisk synkronisering er også trodd å ligge til grunn for de motoriske symptomene i Parkinsons syndrom (Chen, Litvak, Gilbertson, Kuhn, Lu, Lee, Tsai, Tisch, Limousin, Hariz og Brown, 2007). Dermed indikerer forskning at svært rytmisk aktivitet og overdrevet synkronisering kan være patologisk for nervesystemet, særlig for høyere hjernesentre (Erra, Velazquez og Rosenblom, 2017).
Bruk av kompleks systemteori til analyser av EEG-målinger av epilepsi-pasienter tillater en bedret karakterisering av epileptiske hjernetilstander. Slik ikke-lineær EEG-analyse kan bidra til å forbedre evaluering av pasienter før nevrokirurgi. Analysen kan også identifisere og avdekke forløpere til anfall som kan bidra til å utvikle forhindrende teknikker. Ikke-lineær EEG-analyse har også blitt anvendt for analyse av hjerneaktivitet hos OCD-pasienter, hvor både prefrontale og frontotemporale hjerneområder er karakterisert av lavere kompleksitet. Andre studier demonstrerer lavere EEG-kompleksitet i andre angstlidelser, slik som anorexia nevrosa, panikklidelse og PTSD. Man har også funnet redusert kompleksitet hos nevrologiske sykdommer som Alzheimer. En MEG-studie (magnetoencephalography) av Alzheimer-pasienter demonstrerte aktivitet som var mindre kompleks og mer regulativ enn hos kontrollgruppen (Gomez og Hornero, 2010). Resultatene indikerer derfor at kompleksitetsmålinger kan være nyttige også for Alzheimer-diagnostikk. Tidlig deteksjon av abnormaliteter i EEG-signaler kan dessuten være en tidlig biomarkør for kognitive utviklingsforstyrrelser (Bosl, Tierney, Tager-Flusberg og Nelson, 2010). Metoder har blitt utviklet for å skille spedbarn som befinner seg utenom autismespekteret fra spedbarn med høy risiko for å utvikle autisme. Flere studier har demonstrert en sammenheng mellom antall tilknytninger i hjernen og kompleksitet. Mengden kompleksitet i EEG-signaler kan tilby verdifull informasjon om nevrale korrelater for kognitive prosesser.
Konklusjon
I komplekse systemer som hjernen foregår det komplekse interaksjoner mellom deler som sammen gir forekomst av et fenomen. På denne måten er hjernen analogt til en maurkoloni i form av organisert aktivitet som forekommer på tvers av skalaer. Nøkkelen til alle teorier er å vedkjenne fakta og kunne anvende konseptet. Slik George Box har sagt: ”alle modeller er feil, men noen er nyttige” (1997). Når vi har forstått det grunnleggende, er det neste steget å finne ut hvordan man kan anvende det. Nøkkelen til komplekse system er felles påvirkende kausalitet både i og mellom ulike nivå. Dermed er ethvert forsøk på å karakterisere en delvis årsak som helhetlig og eneste årsak, en fundamentalt misvisende posisjon. Man må anerkjenne hele det kausale nettverket som er i operasjon. Man må altså se hele bildet. Vår virkelighet består av både stabilitet og ustabilitet, orden og kaos, noe som har implikasjoner for hvordan vi undersøker og forstår kanskje det viktigste komplekse systemet innenfor psykologien, nemlig hjernen vår.
Referanser
Anderson, P.W. (1972) More is different. Science, Volume 177, nummer 4047. Bak, P., Tang, C. og Wisenfeld, K. (1987) Self-organized criticality: An explanation of the 1/f noise. Physics review. Volume 59, nummer 381. Doi: https://doi.org/10.1103/PhysRevLett.59.381
Bak, P. (1996) How nature works: The science of self-organised criticality. Copernicus. Press, NY. Bendix, H (2013, 15.6) Verden er uforudsigelig: 50 år med kaosteori. Hentet fra: vitenskap.dk
Bosl, W., Tierney, A., Tager-Flusberg, H. Og Nelson, C. (2011) EEG complexity as a biomarker for autism spectrum disorder risk. BMC Medicine, Volum 9, utgave 18.https://doi.org/10.1186/1741-7015-9-18
Chen, C C., Litvak, V, Gilbertson, T., Kuhn, A., Lu C.S, Lee, S. T.,, Tsai, C.H., Tisch, S., Lomuisin, P., Hariz, M., og Brown, P. (2017) Excessive syncronization of basal ganglia neurons at 20 hz slows movement in Parkinsons disease. Experimental Neurology, Volume 205, s. 214-221. Doi: https://doi.org/10.1016/j.expneurol.2007.01.027
Colchester, J (2016, 17.10) Newtonian paradigm (blogginnlegg) Hentet fra:https://complexitylabs.io/newtonian-paradigm/
Di leva, Grizzi, Jelinek, Pellionisz og Losa (2014) Fractals in neuroscience, Part 1: general principles and basic neuroscience. Neuroscientist. Volume 20, nummer 4, s 403 417. Doi: https://doi.org/10.1177/1073858413513927
Dietrichs, E (2007) Hjernens plastisitet – perspektiver for rehabilitering etter hjerneslag.Tidsskrift for Den norske legeforening.
Erra, G. R., Velazquez, J. L. P., og Rosenblom, M. (2017) Neural syncronization from the perspective of non-linear dynamics. Frontiers in computational neuroscience, Volume 11, Nummer 98.
Favela, L.H, Coey, C.A, Griff, E.R og Richardson, M.J (2016) Fractal analysis reveals subclasses of neurons and suggests an explanation of their spontaneous activity. Neuroscience letters, Volume 626, s 54-58.
Frolich, J. (2016) The fugue of life: why complexity matters in neuroscience. Knowing Neurons.
Fryer, P og Ruis, J (2004, 18.6) What are fractal systems? A brief description of complex adaptive and emergent systems (CAES) (blogginnlegg). Hentet fra:http://www.fractal.org/Fractal-Systems.htm
Gomez, C og Hornero, R (2010) Entropy and complexity analyses in Alzheimers Disease:An MEG study. The Open biomedical engineering journal, Volume 4, s. 223-235.Doi: https://dx.doi.org/10.2174%2F1874120701004010223
Guzman, D., Flesia, A, Aon, M., Pellegrini, S., Marin, R og Kembro, J. (2017) The fractal organization of ultradian rhytms in avian behavior. Scientific reports, Volum 7,nummer 684.
Izhikevich, E (2007) Dynamical systems in neuroscience: The geometry of ecxitability andbursting. Massachusetts Institute of Technology. Kandel, E (2016) Reductionism in Art and Brain Science: bridging the two cultures. Columbia University Press, New York.
Kelso, J.A (1995) Dynamic patterns: the self-organization of brain and behavior. MIT press.
Kinni, T (2017, 21.5) The critical difference between complex and complicated. Hentet fra sloanreviewmit.edu
Meisel, C., Storch, A., Hallmeyer-Elgner, S., Bullmore, E., og Gross, T. (2012) Failure of adaptive self-organized criticality during epilepticseizure attacks. PLoSComputational biology. 8:e1002312. doi: 10.1317/journal.pcbi.1002312
Lehnertz, K. (2008) Epilepsy and nonlinear dynamics. Journal of biological physics. Volume 34, nummer 3-4, s. 253-266. Doi:https://dx.doi.org/10.1007%2Fs10867-008-9090-3
Neustadter, E., Mathiak, K og Turetsky, B.I (2016) Chapter 13: EEG and MEG probes of Schizophrenia Pathophysiology. The neurobiology of schizophrenia, s 213-236. Elsevier Inc. Doi: https://doi.org/10.1016/C2014-0-00423-6
Sannita, W. (2008) Neuronal functional diversity and collective behaviours. Journal of Biological Physics. Doi: https://dx.doi.org/10.1007%2Fs10867-008-9097-9
Weiner, S (2018) Why its impossible to accurately measure a coastline. Hentet
fra:https://www.popularmechanics.com/science/environment/a19068718/whyits-impo ssible-to-accurately-measure-a-coastline/
West, G. (2017) Scale: the universal laws of growth, innovation, sustaniability and the pace of life in organisms, cities, economies and companies”. Penguin Press. NY.
Wiesner, K. (2015, 17.12) Brains, bees and bankers.. or why complex systems fail (TED Talk). Hentet fra: https://www.youtube.com/watch?v=mZh_1n8AuuU

